
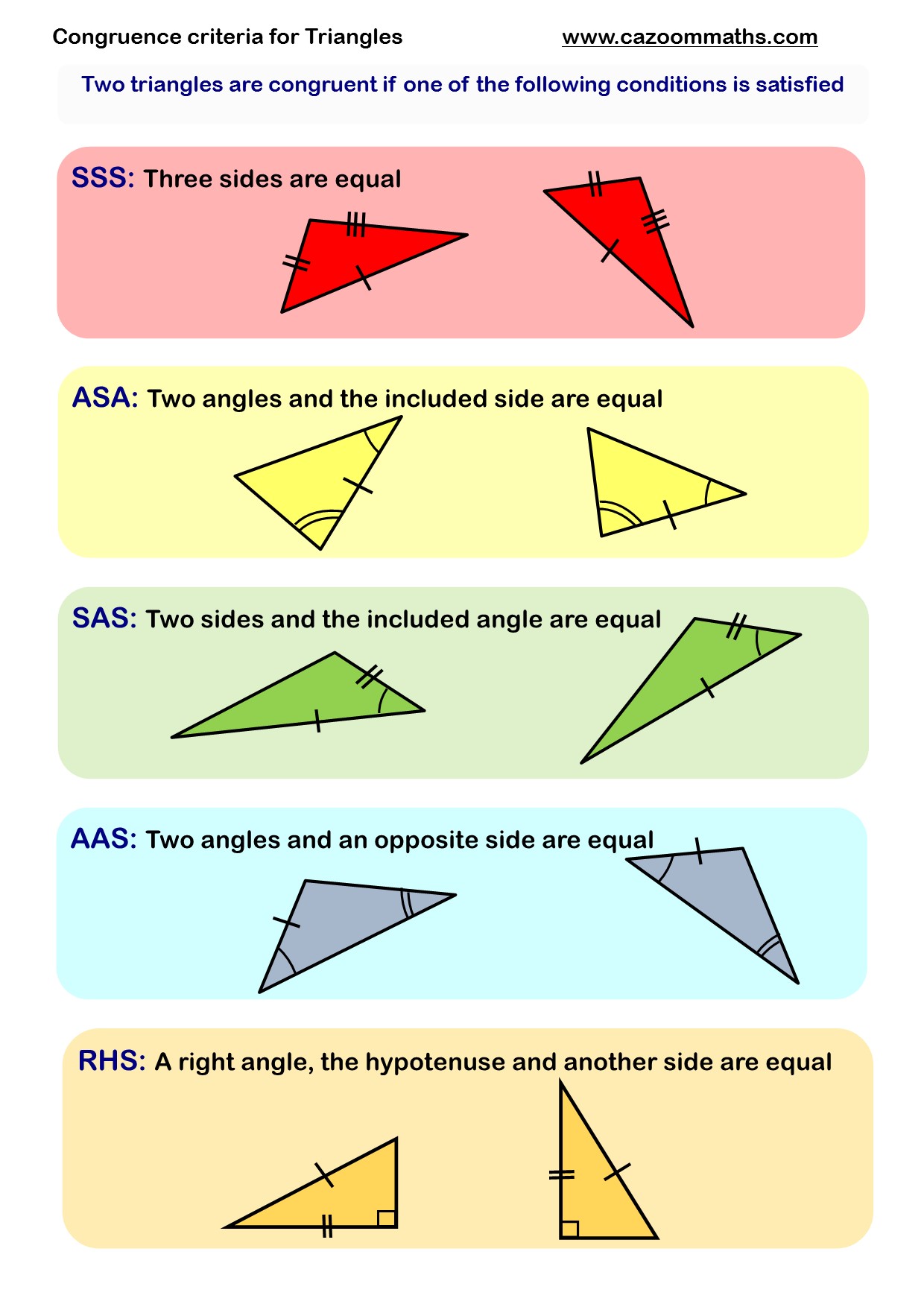
While congruent figures have identical shapes and sizes, similar figures share the same shape but have different sizes. Difference between Congruent Figures and Similar Figures For instance, if two objects A and B are congruent, we can write it as A ≅ B. In geometry, the symbol used to represent congruence is ‘≅.’ This symbol consists of two parts, one above the other, conveying the idea of similarity in shape (represented by the tilde “~”) and equality in size (represented by “=”). For example, if triangle ABC has side lengths AB = EF, AC = EG, and BC = FG, and angles ∠A = ∠E, ∠B = ∠F, and ∠C = ∠G, we can state that triangle ABC ≅ triangle EFG. If all three sides and all three angles of one triangle are congruent to the corresponding sides and angles of another triangle, we can conclude that the triangles are congruent.

To determine congruence in triangles, we need to examine both their side lengths and angles. If Circle A has a radius represented by OR measuring 2 cm and Circle B has a radius represented by OP also measuring 2 cm, we can express their congruence as Circle A ≅ Circle B. Congruent CirclesĬircles are congruent if their radii have equal lengths. For example, if ∠ABC measures 40° and ∠PQR also measures 40°, we can state that ∠ABC ≅ ∠PQR. When two angles have the same measure, they are called congruent angles. For instance, if we have line segment AB measuring 5 cm and line segment PQ measuring 5 cm as well, we can conclude that AB ≅ PQ. In geometry, line segments are considered congruent if their lengths are equal. Congruent Figures: Exploring Examples Congruent Lines Let’s explore each of these in more detail. The concept of congruence applies to various geometric elements, including lines, angles, circles, and triangles. This means that if we place one figure over another, they will perfectly overlap or coincide. What does “Congruent” Mean in Geometry?Ĭongruent figures are defined as objects that have exactly the same shape and size. In this article, we will delve into the meaning of congruent figures, their characteristics, and their importance in geometry. Geometry, a fundamental branch of mathematics, encompasses various concepts that help us analyze and understand the properties of shapes and figures.


 0 kommentar(er)
0 kommentar(er)
